NCERT CLASS 10 MATHS SOLUTIONS CHAPTER-3(3.2)

NCERT CLASS 10 MATHS SOLUTIONS

CHAPTER-3 दो चर वाले रैखिक समीकरण युग्म

प्रश्नावली 3.2

आप इस प्रश्नावली को समझने के लिए नीचे दी गई सारणी को समझे-

अगर आपकी दी गई रैखिक समीकरण युग्म a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 प्रकार का है ,तो

क्र.सं.	अनुपातों की तुलना	ग्राफीय निरूपण	ग्राफीय चित्र	बीजगणितीय निरूपण
1.	$\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$	प्रतिच्छेद करती हुई रेखाऐं	×	केवल एक हल (अद्वितीय )
2.	$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$	सम्पाती रेखाएँ	↔	अपरिमित रूप से अनेक हल
3.	$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$	समांतर रेखाएँ	//	कोई हल नहीं

प्रश्न 1: निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफ़िय विधि से हल ज्ञात कीजिए।

(i) कक्षा x के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या

लड़कों की संख्या से 4 अधिक हो ,तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।

हल: माना कि लड़कों की संख्या x व लड़कियों की संख्या y है।

∴प्रश्नानुसार ,

x+y = 10 ….(1) (क्योंकि कुल विद्यार्थी 10 है।)

तथा x+4 =y (क्योंकि लड़कियों की संख्या लड़को की संख्या से 4 अधिक है।)

या x−y =−4 ….(2)

समीकरण (1) में x के मान क्रमशः 4,5 व 6 रखने पर

y के मान क्रमशः 6 ,5 व 4 प्राप्त होते है।

अतः प्राप्त सारणी

x	4	5	6
y	6	5	4

समीकरण (2) में x के मान क्रमशः 0,1 व 2 रखने पर

y के मान क्रमशः 4, 5 व 6 प्राप्त होते है।

अतः प्राप्त सारणी

x	0	1	2
y	4	5	6

ग्राफ से स्पष्ट है कि रेखाएँ बिंदु (3,7) पर प्रतिच्छेद करती है।

अर्थात कक्षा में लड़कों की संख्या 3 व लड़कियों की संख्या 7 है।

(ii) 5 पेंसिल तथा 7 कलमों का कुल मूल्य 50 रु है ,जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य 46 रु है।

एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए।

हल:माना कि एक पेंसिल का मूल्य x रु व एक कलम का मूल्य y रु है।

तब प्रश्नानुसार, स्थिति-I

5x+7y = 50

या $x=\frac{50-7y}{5}$ ….(1)

तथा स्थिति-II

7x+5y = 46

या $x=\frac{46-5y}{7}$ ….(2)

समीकरण (1) में y के मान क्रमशः0 ,5 व 10 रखने पर

x के मान क्रमशः 10 , 3 व −4 प्राप्त होते है।

अतः प्राप्त सारणी

x	10	3	−4
y	0	5	10

समीकरण (2) में y के मान क्रमशः 5 ,−2 व −9 रखने पर

x के मान क्रमशः 3 ,8 व 13 प्राप्त होते है।

अतः प्राप्त सारणी

x	3	8	13
y	5	−2	−9

ग्राफ से स्पष्ट है कि रेखाएँ बिंदु (3,5) पर प्रतिच्छेद करती है।

अर्थात एक पेंसिल का मूल्य 3 रु व एक कलम का मूल्य 5 रु है।

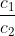प्रश्न 2: अनुपातों $\frac{a_{1}}{a_{2}},\frac{b_{1}}{b_{2}}$ और $\frac{c_{1}}{c_{2}}$ की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाऐं

एक बिंदु पर प्रतिच्छेद करती है ,समांतर है अथवा सम्पाती है :

(i) 5x−4y+8 = 0

7x+6y−9 = 0

(ii) 9x+3y+12 = 0

18x+6y+24 = 0

(iii) 6x−3y+10 = 0

2x −y+9 = 0

प्रश्न 2:हल:(i)

5x−4y+8 = 0

7x+6y−9 = 0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=5 ,b₁=−4 व c₁=8 तथा

a₂=7 ,b₂=6 व c₂=−9

∴ $\frac{a_{1}}{a_{2}}=\frac{5}{7}, \frac{b_{1}}{b_{2}}=\frac{-4}{6}or\frac{-2}{3}, \frac{c_{1}}{c_{2}}=\frac{8}{-9}$

यहाँ $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$

∴ दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं एक बिंदु पर प्रतिच्छेद करती है।

प्रश्न 2:हल:(ii)

9x+3y+12 = 0

18x+6y+24 = 0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=9 ,b₁=3 व c₁=12 तथा

a₂=18 ,b₂=6 व c₂=24

∴ $\frac{a_{1}}{a_{2}}=\frac{9}{18} or \frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{3}{6}or\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{12}{24}or\frac{1}{2}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं सम्पाती है।

प्रश्न 2:हल:(iii)

6x−3y+10 = 0

2x −y+9 = 0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=6 ,b₁=−3 व c₁=10 तथा

a₂=2 ,b₂=−1 व c₂=9

∴ $\frac{a_{1}}{a_{2}}=\frac{6}{2}or 3 ,\frac{b_{1}}{b_{2}}=\frac{-3}{-1}or3, \frac{c_{1}}{c_{2}}=\frac{10}{9}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं समान्तर है।

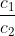प्रश्न 3: अनुपातों $\frac{a_{1}}{a_{2}},\frac{b_{1}}{b_{2}}$ और $\frac{c_{1}}{c_{2}}$ की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत है या असंगत :

(i) 3x+2y = 5 ; 2x−3y = 7

(ii) 2x−3y = 8 ; 4x−6y = 9

(iii) $\frac{3}{2}x+\frac{5}{3}y=7$ ; 9x−10y =14

(iv) 5x−3y =11 ; −10x+6y =−22

(v) $\frac{4}{3}x+2y=8 ; 2x+3y=12$

प्रश्न 3:हल:(i)

3x+2y = 5 ; 2x−3y = 7

दी गई रैखिक समीकरण युग्म को पुनर्व्यवस्थित करने पर

3x+2y −5=0 ; 2x−3y −7=0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=3 ,b₁=2 व c₁=−5 तथा

a₂=2 ,b₂=−3 व c₂=−7

∴ $\frac{a_{1}}{a_{2}}=\frac{3}{2},\frac{b_{1}}{b_{2}}=\frac{2}{-3},\frac{c_{1}}{c_{2}}=\frac{-5}{-7}$

यहाँ $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$

∴ दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं एक बिंदु पर प्रतिच्छेद करती है।

अर्थात दी गई समीकरण युग्म संगत है।

प्रश्न 3:हल:(ii)

2x−3y = 8 ; 4x−6y = 9

दी गई रैखिक समीकरण युग्म को पुनर्व्यवस्थित करने पर

2x−3y −8=0 ; 4x−6y−9=0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=2 ,b₁=−3 व c₁=−8 तथा

a₂=4 ,b₂=−6 व c₂=−9

∴ $\frac{a_{1}}{a_{2}}=\frac{2}{4}or\frac{1}{2},\frac{b_{1}}{b_{2}}=\frac{-3}{-6}or\frac{1}{2},\frac{c_{1}}{c_{2}}=\frac{-8}{-9}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं समान्तर है।

अर्थात दी गई समीकरण युग्म असंगत है।

प्रश्न 3:हल:(iii)

$\frac{3}{2}x+\frac{5}{3}y=7$ ; 9x−10y =14

दी गई रैखिक समीकरण युग्म को पुनर्व्यवस्थित करने पर

9x+10y −42 =0 (कैसे?) (पहली समीकरण के प्रत्येक पद को 6 से गुणा करने पर)

तथा 9x −10y −14=0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=9 ,b₁=10 व c₁=−42 तथा

a₂=9 ,b₂=−10 व c₂=−14

∴ $\frac{a_{1}}{a_{2}}=\frac{9}{9}or1,\frac{b_{1}}{b_{2}}=\frac{10}{-10}or-1,\frac{c_{1}}{c_{2}}=\frac{-42}{-14}or3$

यहाँ $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$

∴ दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं एक बिंदु पर प्रतिच्छेद करती है।

अर्थात दी गई समीकरण युग्म संगत है।

प्रश्न 3:हल:

(iv) 5x−3y =11 ; −10x+6y =−22

दी गई रैखिक समीकरण युग्म को पुनर्व्यवस्थित करने पर

5x−3y−11=0 ; −10x+6y+22=0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=5 ,b₁=−3 व c₁=−11 तथा

a₂=−10 ,b₂=6 व c₂=22

∴ $\frac{a_{1}}{a_{2}}=\frac{5}{-10}or\frac{-1}{2},\frac{b_{1}}{b_{2}}=\frac{-3}{6}or\frac{-1}{2},\frac{c_{1}}{c_{2}}=\frac{-11}{22}or\frac{-1}{2}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं सम्पाती है।

अर्थात दी गई समीकरण युग्म संगत है।

प्रश्न 3:हल: (v)

$\frac{4}{3}x+2y=8 ; 2x+3y=12$

दी गई रैखिक समीकरण युग्म को पुनर्व्यवस्थित करने पर

4x+6y −24 =0 (कैसे?) (पहली समीकरण के प्रत्येक पद को 3 से गुणा करने पर)

तथा 2x+3y−12=0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=4 ,b₁=6 व c₁=−24 तथा

a₂=2 ,b₂=3 व c₂=−12

∴ $\frac{a_{1}}{a_{2}}=\frac{4}{2}or2,\frac{b_{1}}{b_{2}}=\frac{6}{3}or2,\frac{c_{1}}{c_{2}}=\frac{-24}{-12}or2$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं सम्पाती है।

अर्थात दी गई समीकरण युग्म संगत है।

प्रश्न 4: निम्न रैखिक समीकरणों के युग्मो में से कौन से युग्म संगत/असंगत है ,यदि संगत है तो ग्राफीय विधि से हल ज्ञात कीजिए।

(i) x +y = 5 , 2x +2y =10

(ii) x −y = 8 , 3x −3y = 16

(iii) 2x +y −6 = 0 , 4x −2y −4 = 0

(iv) 2x −2y −2 = 0 , 4x −4y −5 = 0

प्रश्न 4:हल:(i)

x +y = 5 …(1)

2x +2y =10

(प्रत्येक पद में 2 का भाग देने पर)

या x +y = 5 …(2)

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=1 ,b₁=1 व c₁=5 तथा

a₂=1 ,b₂=1 व c₂=5

∴ $\frac{a_{1}}{a_{2}}=\frac{1}{1}or1,\frac{b_{1}}{b_{2}}=\frac{1}{1}or1,\frac{c_{1}}{c_{2}}=\frac{5}{5}or1$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं सम्पाती है।

अर्थात दी गई समीकरण युग्म संगत है।

इसका ग्राफीय हल निम्नानुसार है-

समीकरण (1) व (2) में y के मान क्रमशः1 ,2 व 3 रखने पर

x के मान क्रमशः 4 , 3 व 2 प्राप्त होते है।

अतः प्राप्त सारणीयां

x	4	3	2
y	1	2	3

तथा

x	4	3	2
y	1	2	3

ग्राफ से स्पष्ट है कि दी गई रैखिक समीकरण युग्म के अनेक हल विध्यमान है।

प्रश्न 4:हल:(ii) x −y = 8 , 3x −3y = 16

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=1 ,b₁=1 व c₁=−8 तथा

a₂=3 ,b₂=3 व c₂=−16

∴ $\frac{a_{1}}{a_{2}}=\frac{1}{3},\frac{b_{1}}{b_{2}}=\frac{1}{3},\frac{c_{1}}{c_{2}}=\frac{-8}{-16}or\frac{1}{2}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं समान्तर है।

अर्थात दी गई समीकरण युग्म असंगत है।

प्रश्न 4:हल:(iii)

2x +y −6 = 0 …(1)

4x −2y −4 = 0 …(2)

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=2 , b₁=1 व c₁=−6 तथा

a₂=4 , b₂=−2 व c₂=−4

∴ $\frac{a_{1}}{a_{2}}=\frac{2}{4}or\frac{1}{2},\frac{b_{1}}{b_{2}}=\frac{1}{-2},\frac{c_{1}}{c_{2}}=\frac{-6}{-4}or\frac{3}{2}$

यहाँ $\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$

∴ दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं एक बिंदु पर प्रतिच्छेद करती है।

अर्थात दी गई समीकरण युग्म संगत है।

इसका ग्राफीय हल निम्नानुसार है-

समी (1) से y=6−2x

उपरोक्त समी. में x का मान 1,2 व 3 रखने पर ,

y का मान क्रमशः 4,2 व 0 प्राप्त होता है।

अतः प्राप्त सारणी

x	1	2	3
y	4	2	0

समी. (2) से y=2x−2

उपरोक्त समी. में x के मान क्रमशः 1,2 व 3 रखने पर

y के मान क्रमशः 0 ,2 व 4 प्राप्त होते है।

अतः प्राप्त सारणी

x	1	2	3
y	0	2	4

ग्राफ से स्पष्ट है कि दी गई रैखिक समीकरण युग्म का हल (2,2) है।

प्रश्न 4:हल:(iv) 2x −2y −2 = 0 , 4x −4y −5 = 0

दी गई समीकरण युग्म की तुलना a₁x +b₁y +c₁=0 तथा a₂x +b₂y +c₂= 0 से करने पर

a₁=2 , b₁=−2 व c₁=−2 तथा

a₂=4 , b₂=−4 व c₂=−5

∴ $\frac{a_{1}}{a_{2}}=\frac{2}{4}or\frac{1}{2},\frac{b_{1}}{b_{2}}=\frac{-2}{-4}or\frac{1}{2},\frac{c_{1}}{c_{2}}=\frac{-2}{-5}or\frac{2}{5}$

यहाँ $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

∴दी गई समीकरण युग्म द्वारा निरूपित रेखाऐं समान्तर है।

अर्थात दी गई समीकरण युग्म असंगत है।

प्रश्न 5: एक आयताकार बाग ,जिसकी लम्बाई ,चौड़ाई से 4m अधिक है ,का अर्धपरिमाप 36 m है। बाग की विमाएँ ज्ञात कीजिए।

हल: माना कि आयताकार बाग की लम्बाई x मीटर व चौड़ाई y मीटर है।

तब प्रश्नानुसार,

x =y +4 (कैसे?)(क्योंकि लम्बाई ,चौड़ाई से 4m अधिक है।)

या x −y =4 …(1)

तथा

x +y=36 ….(2) (कैसे?)(क्योंकि अर्धपरिमाप 36 m है।)

समी.(1)+समी.(2) से,

2x =40 या x =20

x का ये मान समी.(2) में रखने पर

20+y =36

या y =16

अतः दिए गए आयताकार बाग की लम्बाई 20 मीटर व चौड़ाई 16 मीटर है।

प्रश्न 6:एक रैखिक समीकरण 2x +3y −8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का

ज्यामितीय निरूपण जैसा कि

(i) प्रतिच्छेद करती रेखाएँ हो।

(ii) समांतर रेखाएँ हो।

(iii) सम्पाती रेखाएँ हो।

हल: (i) प्रतिच्छेद करती रेखाएँ हो।

हम जानते है कि रेखाएँ प्रतिच्छेद करेगी यदि

$\frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}}$

अतः एक रेखा 2x +3y −8 = 0 है तो,

दूसरी रेखा 3x +2y −6 = 0 हो सकती है।

हल: (ii) समांतर रेखाएँ हो।

हम जानते है कि रेखाएँ समान्तर होगी यदि

$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$

अतः एक रेखा 2x +3y −8 = 0 है तो,

दूसरी रेखा 4x +6y −9 = 0 हो सकती है।

हल: (iii) सम्पाती रेखाएँ हो।

हम जानते है कि रेखाएँ सम्पाती होगी यदि

$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

अतः एक रेखा 2x +3y −8 = 0 है तो,

दूसरी रेखा 4x +6y −16 = 0 हो सकती है।

प्रश्न 7 : समीकरणों x −y +1 = 0 और 3x +2y −12 = 0 का ग्राफ खींचिए। x अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक

ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।

हल: दी गई समीकरणों से

x−y+1=0

या x =y−1 …(1)

तथा 3x +2y −12 = 0

या $x=\frac{12-2y}{3}$ …(2)

समीकरण (1) में y के मान क्रमशः0 ,1 व 2 रखने पर

x के मान क्रमशः −1 , 0 व 1 प्राप्त होते है।

अतः प्राप्त सारणी

x	−1	0	1
y	0	1	2

समीकरण (2) में y के मान क्रमशः 0 ,3 व 6 रखने पर

x के मान क्रमशः 4 ,2 व 0 प्राप्त होते है।

अतः प्राप्त सारणी

x	4	2	0
y	0	3	6

अतः ग्राफ निम्नानुसार होगा

ग्राफ से स्पष्ट है कि x अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक

(2,3) , (4,0) व (-1,0) है।